2017考研数学常考题型之导数定义的应用
一元函数微分学是组成微积分的重要一部分,而对于导数的和微分这一部分的两个重要的概念,对于它们的概念不仅要理解,而且还要挖掘其定义的内涵,尤其是导数的定义,几乎是每年考研中必考的。而对于它的定义得应用在考研中有所体现,下面文都教育李老师带领大家一起来看看.
导数的定义是通过极限给出了函数在某一点可导的定义,并且此极限值就是函数在该点处的定义. 下面来看看导数定义的应用.
第一,判断函数在某点的可导性. 一般有两种方法.
方法1:常利用导数定义及导数在一点存在的充要条件(左、右导数存在且相等)来进行讨论之.常常从四个方面进行考察:
(1)自变量的趋向过程是否加了限制,该过程是半过程还是全过程;
(2)函数值的差值中是否含有可待判断的点处的函数值;
(3)函数差值中的自变量改变量与分母中的自变量改变量是否完全一致;
(4)左、右导数是否都存在且相等.
方法2:利用下述命题讨论函数在某点的可导性.


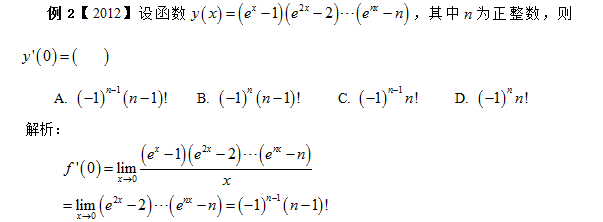
对于导数的定义看着较为简单,但是要做到对导数定义的深刻理解以及灵活应用,有着一定的难度,因为有时本来是求极限的题目,但是却往往最后仍然归结为导数定义的应用和计算. 希望同学们在后期的复习过程中,也可以自己多归纳,多总结,找到做题的方法和技巧.




